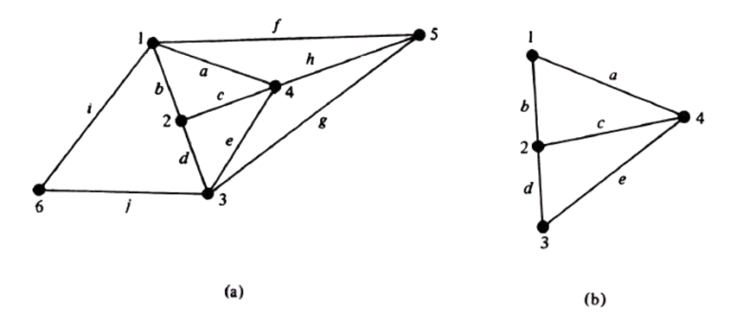
Sub Graphs  

Sub-Graph

A graph g is said to be a subgraph of a graph G if all the vertices and all the edges of g are in G, and each edge of g has the same end vertices in g as in G.

A subgraph can be thought of as being contained in (or a part of) another graph. The symbol from set theory, g ⊂ G, is used in stating “g is a subgraph of G.”

The following observations can be made immediately:

1. Every graph is its own subgraph.

2. A subgraph of a subgraph of G is a subgraph of G.

3. A single vertex in a graph G is a subgraph of G.

4. A single edge in G, together with its end vertices, is also a subgraph of G

Edge-Disjoint Subgraphs:

·        Two (or more) subgraphs g1 and g2 of a graph G are said to be edge disjoint if g1 and g2 do not have any edges in common.

Vertex-Disjoint Subgraphs:

·        Sub graphs that doesn’t even have vertex in common are said to be vertex disjoint.