Isomorphism  

Isomorphism

·        Two graphs are thought of as equivalent (and called isomorphic) if they have identical behaviour in terms of graph-theoretic properties.

·        Two graphs G and G′ are said to be isomorphic (to each other) if there is a one-to-one correspondence between their vertices and between their edges such that the incidence relationship is preserved.

·        In other words, suppose that edge e is incident on vertices v1 and v2 in G; then the corresponding edge e′ in G′ must be incident on the vertices v′1 and v′2 that correspond to v1 and v2, respectively.

For example, one can verify that the two graphs in Fig. 2-1 are isomorphic. The correspondence between the two graphs is as follows: The vertices a, b, c, d, and e correspond to v1 , v2 , v3 , v4 , and v5 , respectively. The edges 1, 2, 3, 4, 5, and 6 correspond to e1 , e2 , e3 , e4 , e5 , and e6 , respectively.

Isomorphic graphs must have

·        Same number of edges

·        Same number of vertices

·        Equal number of vertices with the given degree

 

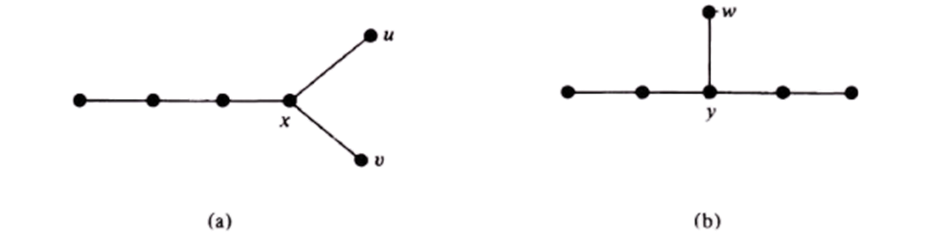
For instance, the two graphs shown in Figure satisfy all three conditions, yet they are not isomorphic.

·        That the graphs in Figs.(a) and (b) are not isomorphic can be shown as follows: If the graph in Fig. (a) were to be isomorphic to the one in (b), vertex x must correspond to y, because there are no other vertices of degree three.

·        Now in (b) there is only one pendant vertex, w, adjacent to y, while in (a) there are two pendant vertices, u and v, adjacent to x.