Finite and Infinite Graph
Define
·
Finite Graphs:
o
A finite graph is a graph that has a finite
number of vertices and edges.
o
In a finite graph, both the set of vertices (V)
and the set of edges (E) are finite.
o
Examples of finite graphs include social
networks with a limited number of users, road networks within a city, or any
graph that involves a finite set of objects or entities.
§
·
Infinite Graphs:
o
An infinite graph is a graph that has an
infinite number of vertices and/or edges.
o
Infinite graphs can have either an infinite set
of vertices (V), an infinite set of edges (E), or both.
o
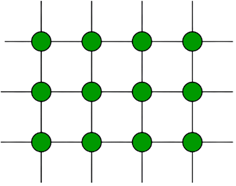
Examples of infinite graphs include:
§
Infinite Grid: A grid with vertices at every
integer coordinate point (e.g., the integer lattice in the plane).
§
Isolated Vertex:
·
An isolated vertex is a vertex in a graph that
is not connected to any other vertex in the graph. In other words, it has no
edges incident to it.
·
Isolated vertices are often represented as
standalone points within a graph, with no lines (edges) connecting them to other
points.
o
Pendant
Vertex:
·
A pendant vertex is a vertex in a graph that is
connected to exactly one other vertex. It has a single edge (pendant edge)
connecting it to another vertex.
·
Pendant vertices can be thought of as
"hanging" from another vertex, as they have only one connection.
o
Null Graph:
·
A null graph, also known as an empty graph, is a
graph that has no vertices and, consequently, no edges. It is the simplest
possible graph.
·
In mathematical notation, a null graph is often
denoted as G = (V, E), where V is the empty set (no vertices) and E is also the
empty set (no edges).
·
The edge set ‘E’ may be empty but, the vertex
set ‘V’ must not be empty, otherwise, there is no graph’s, so, a graph must
have at least one vertex.
o